Surgical Treatment Plan

Before surgery is planned, the surgeon must determine whether the patient is ready for surgery. This entails confirming that the goals of presurgical orthodontics have been met and that the patient’s health has been optimized to ensure the lowest possible surgical risk.
Surgeons obtain progress-dental-models to determine that the goals of presurgical orthodontics have been met. They hand-articulate the models in Class I occlusion to confirm that good occlusion is achievable. Good occlusion can be achieved when:
- Dental compensations have been eliminated
- The teeth are well aligned, forming a smooth arch
- The shape and size of the upper and lower dental arches match
- Adjacent marginal ridges are leveled
- Interproximal spaces are closed (unless spacing is needed to compensate for a discrepancy in tooth size)
- The curve of Spee is flat or minimal
- The labiolingual inclination of posterior teeth is normal
- The incisal overjet and overbite are normal
- The tooth size discrepancies (Bolton) have been dealt with
- Occlusal contacts are maximized
If good intercuspation is observed and the risks of surgery are acceptable, the patient is ready for surgery.
Occasionally, good intercuspation cannot be achieved because of the presence of an apical base deformity. The apical base is the part of the jawbones located around the apices of teeth, and it determines the position of the dental roots. Because dental roots should not be moved outside the bone, maximal intercuspation cannot be achieved when the apical bases are deformed. For example, when the maxillary apical base is narrow the posterior teeth will end in crossbite, despite adequate presurgical orthodontics. In such cases, the maxilla must be segmented—separated into two or more tooth-bearing bone segments—so that it can be expanded.
If good intercuspation cannot be achieved because of an apical-base problem, the surgeon should segment the dental models to determine whether good occlusion is achievable. When dental models are cut into segments, each piece is hand-articulated into occlusion and the segments are then reassembled and glued. If the surgeon confirms that this operation can be safely performed on the patient, then he/she is deemed to be ready for surgery.
It is important to note that jaw segmentation should not, routinely, be used to compensate for poor orthodontics. In the absence of apical base problems, poor Class I intercuspation indicates that presurgical orthodontics should continue. In some cases, however, the goal of presurgical orthodontics is not maximal intercuspation. For example, in patients with deep-bite Class II malocclusion, with a deep curve of Spee and a short anterior mandibular height, it may be best not to level the curve of Spee prior to surgery, because this may result in intrusion of the anterior teeth and additional vertical foreshortening of the anterior mandible. A better approach may be to perform surgery before the curve of Spee is leveled. At surgery, the occlusion is set to a normal incisal overbite, with occlusal contacts limited to the incisors and second molars. Postoperatively, an orthodontist levels the mandibular occlusal plane by erupting the premolars, limiting intrusion of the lower incisors.
Once the decision has been made to proceed with surgery, surgical planning begins. A surgeon devises an orthognathic operation by simulating the surgical procedures and visualizing their outcomes. This process is iterated until the desired results are visualized. The approach is called the Visualized Treatment Objective (VTO), a term denoting that the plan is developed by visualizing the final outcome (i.e., the treatment objective).
With VTO, the operation is simulated with models that reproduce the craniofacial anatomy. Traditional planning methods have utilized two-dimensional line drawings of plain cephalograms and stone dental models mounted on a dental articulator; such methods have significant limitations6, 7, 10, 30-32 and, fortunately, are being phased out. This chapter presents a Computer-Aided Surgical Simulation (CASS) method, 10, 33 which has three phases: modeling, planning, and preparing for plan execution.
Modeling
In the modeling phase, one creates a 3D virtual model of the craniofacial complex. This model should:
- Have a mandible in centric relationship;
- Accurately render the skeleton, the teeth, and the facial soft-tissue; and
- Have a correct frame of reference.
3D virtual models used for CASS should have a mandible in centric relationship. Centric relationship (CR) is the position in which the condyles are centered within the glenoid fossae. It is an important reference position in orthognathic surgery, as it is the only tooth-independent mandibular position that is reproducible.10, 34, 35 Moreover, in this position, the condyles can rotate for about 20 degrees around an axis that passes near the center of both condyles.36, 37 Rotation of the mandible around this hinge axis is called autorotation.
Having a virtual model in CR is necessary in single jaw maxillary surgery and bimaxillary surgery, if the maxilla is cut first. In these operations, the mandible dictates the location of the maxilla, thus, any discrepancy in mandibular position between the virtual model and the patient results in postoperative outcomes that are different from the initial plan. At surgery, the mandible will always be placed in CR; the virtual model should have the same position. Occasionally, before surgery, it is impossible to place the patient in CR (e.g., patients with severe micrognathia). With such patients, the surgeon should consider performing mandibular surgery first, as this obviates the need for accurate CR recording.34, 38
Another important feature of 3D virtual models is that they should render the skeleton, the teeth, and the soft-tissue well. Computerized tomography (CT) scans can be used to create 3D models of the craniofacial skeleton, teeth, and soft-tissue. Yet, with these models, the teeth are not sufficiently accurate for the purposes of surgical planning.30, 39-41 The CASS protocol solves this problem by replacing the inaccurate teeth of the CT with accurate digital dental models.39 Dental impressions or stone dental models are scanned via optical scanner, a micro-CT, or a cone beam CT to create these models. A model created by merging a CT with digital dental models is called a composite model.33, 39
The process of aligning digital dental models with the CT scan is called registration. It is done by aligning corresponding features that are present in both images. Different algorithms have been developed for this purpose. In these algorithms, the corresponding features can be points (i.e., landmarks),39, 42 surfaces,43 or volumes.44 They can be part of the structures being imaged or they can be fiducial markers—easy to identify parts that are placed in, on, or around the objects before image capture.45.
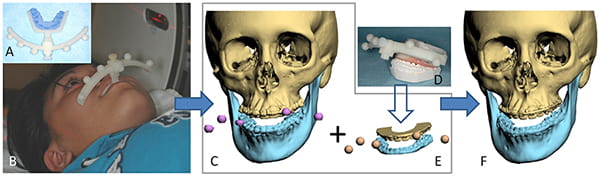
Gateno, Xia, et al. have developed and validated a fiducial registration system for making composite models.39 In addition to enabling accurate registration, the system ensures that the mandible is in CR during scanning, which is a key feature.10, 34 Presented Figure 20, this system uses a two-part device consisting of a bite-jig and a fiducial-facebow.
The bite-jig has a dual purpose: it anchors the facebow to the patient and keeps the mandible in CR during image acquisition. It consists of a customizable stock frame with an anterior male coupler. To customize the jig, a clinician first adds self-cured rigid bite registration material to the frame and subsequently places the jig between the teeth until the material is cured. During bite registration, the clinician seats the mandible into CR.
The plastic facebow attaches to the bite-jig through a female coupler. The facebow has a set of fiducial markers that is used for registration. Before CT scanning, the device—consisting of a bite-jig and a facebow—is assembled and affixed to the patient. A CT scan is then taken while the patient is biting on the device. The resultant images portray the facial anatomy, as well as the fiducial markers.
Subsequently, the same device is placed between stone dental models (upper and lower); the models are then scanned. This creates a set of digital dental models surrounded by fiducial markers. In the last step, the digital dental models are registered by the CT, creating a composite model.
As referenced above, a 3D virtual model of the craniofacial skeleton should accurately render the facial soft-tissues. Moreover, it should depict a relaxed position. This is accomplished by asking the patient not to animate his/her face during image capture; also note that deformations produced by posture or external sources should be avoided. Examples of deformities that produce postures resulting in soft-tissue distortion include curling of the lower lip by the upper incisor in Class II deep-bite malocclusions, pouting of the lips from overclosure in vertical maxillary deficiency, downward concavity of the upper vermillion in vertical maxillary excess, and severe anterior open bite. The first two deformations can be avoided by opening the bite, but the latter is unavoidable. As mentioned previously, external sources (e.g., chin-rests, forehead holders, bite-jigs, dental trays, etc.) can also deform the soft-tissues.
Virtual models used for planning must have an accurate anatomic frame of reference, as this frame constitutes the basis of most decisions during planning. An incorrectly defined frame of reference can result in postoperative deformity. One can erect a frame of reference for a 3D model by using one of two approaches: anatomical landmarks or the NHP.
The first method uses anatomic landmarks to create a Cartesian frame. At first glance, the task seems trivial. The planner constructs the median plane using any three midline-landmarks. He then makes the axial plane Frankfort horizontal plane, and constructs Frankfurt using 3 of the 4 points that define it (right orbital, left orbital, right porion, and left porion). Finally, he builds the coronal plane, making it pass through both porions, keeping it perpendicular to the other two planes.
Notwithstanding, this simple method only works when the face is perfectly symmetrical. In facial asymmetry, various combinations of three midline landmarks produce different median planes. For the same reason, various combinations of Frankfort points result in different axial planes. Moreover, in facial asymmetry, the Frankfort horizontal is usually not perpendicular to the median plane—a fundamental requirement of the Cartesian system. Finally, a coronal plane cannot be constructed if the two other planes (median and axial) are not perpendicular. Thus, as all faces have some degree of asymmetry, using landmarks to build a frame of reference is highly complex.
The orthogonal best-fit method is an approach that takes into consideration the universal asymmetry of the face and the requirement of perpendicularity among the planes. A computer algorithm constructs three orthogonal planes, minimizing the distance between those planes and key facial landmarks. The median plane is the best-fit plane for all midline landmarks, the axial plane is the best-fit plane for the Frankfort landmarks, and the coronal plane is the best-fit plane for both porions. However, as explained below, this method is also flawed.
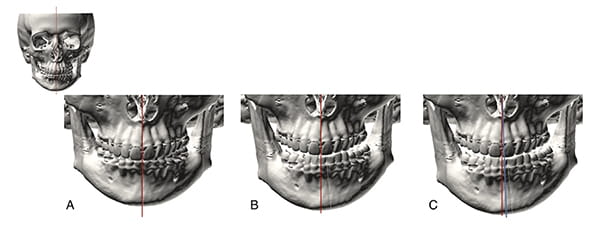
One example that illustrates why the orthogonal best-fit method is unsatisfactory is depicted in Figure 21-A, which shows the 3D CT scan of a hypothetical subject with perfect facial symmetry. In the ensuing year, the patient develops right condylar hyperplasia, resulting in left chin deviation. The rest of her face, including the maxilla, remains unchanged (Figure 21-B). After developing the asymmetry, she seeks treatment. A surgeon sees her and conducts a 3D-CT. He calculates the median plane of the head using the orthogonal best-fit method (depicted as a blue line in Figure 21-C). This method would identify the median plane as the plane that best fits all midline landmarks, but because some midline landmarks are deviated (i.e., the mandible), the median plane will be skewed. Making assessments based on this skewed plane, the surgeon would incorrectly conclude that the maxilla is deviated to the right and the chin is deviated to the left—when, in reality, the maxilla is normal and only the chin is off.
Why is this the case? Some of the landmarks used by the algorithm are affected by asymmetry. In this instance, the shifted mandibular landmarks skewed the median plane. Thus, one should conclude that facial asymmetries render the landmark method invalid. Moreover, this simple theoretical example caused the authors to reconsider the essence of the anatomical frame of reference, particularly when it involves asymmetry. After some reflection, it is now understood that the anatomical frame of reference a clinician requires is the one a patient would have if he or she did not have an asymmetry: the primal frame of reference.
In the hypothetical case presented above, the primal frame of reference can be easily calculated by excluding the skewed mandibular landmarks. Viewed from this perspective, our previous case is simple, as the remainder of the facial skeleton is symmetric. However, when all facial and cranial structures are grossly asymmetric, how does one calculate the frame of reference? A second method that can be used to create an anatomical frame of reference for the entire head—the natural head posture—can solve this problem.
The principle behind using the natural head posture (NHP) is that the primal frame of reference of the head can be derived from this posture. When humans stand erect, looking straight forward, the cardinal directions of their faces are orthogonal to gravity. The axial plane is perpendicular to gravitational pull and the median and coronal planes are aligned with it. Thus, when the head is in the NHP, constructing a frame of reference for the face is simple. The axial plane is the horizontal plane that passes through both porions. The median plane is the vertical plane that best divides the face into right and left halves. The coronal plane is the vertical plane that is perpendicular to the other planes and aligned with the coronal suture.
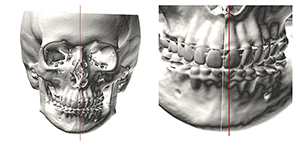
Since the NHP is unaltered by developing jaw asymmetries, the frames of reference calculated by this method are unaffected by such deformities. Unfortunately, NHP is inconsistent for two reasons. First, some patients have difficulty aligning their heads in the NHP. This is especially true of children, patients with neuromuscular problems, patients with torticollis, and patients with eye muscle imbalances. Second, even within the same patient, there are temporal variations in the NHP. When one records the NHP on the same patient, at various intervals, one obtains different measurements. Most of the time, the measurements are in close proximity, varying within two degrees—yet, even these small variations are problematic. Figure 22 presents the example of a symmetric patient who rolled his head (around nasion) by two degrees during NHP recording. This small error caused the upper incisal midpoint and pogonion to appear right-deviated—the upper incisal midpoint by 1.6 mm and pogonion by 2.6mm—when they were not. These are significant errors.
There are two ways of orienting a CT scan to the NHP. One is to scan the head while in the NHP; the other is to scan the head in any orientation and then reorient the resultant image to the NHP. CT scanners are aligned with the world, an alignment that takes into consideration the orientation of the patient’s body during scanning (i.e., supine or erect). If we place a patient in the NHP during CT acquisition—or its equivalent for a supine patient—the resultant image will automatically be in the NHP. Although this method seems simple, in practice it is difficult to implement. In medical CT scanners, it is hard to set the head in the NHP when the patient is supine. In a cone-beam CT scanner, where patients sit, chin-rests and head-holders commonly interfere with the NHP. Therefore, reorienting images into the NHP after CT acquisition is ultimately more practical.
Three methods can be used to reorient a randomly oriented 3D CT to the NHP: 1) standardized photographs,10 2) laser levels,46, 47 and 3) orientation sensors.10-12
In the first method, standardized frontal and lateral facial photographs taken with the patient in the NHP serve as visual guides to manually reorient the 3D CT in the computer. Although this method is subjective, it is valuable for checking the outcome of advanced methods.
In the second method, a patient is placed in the NHP. Then, the perpendicular lights of a laser-level are projected onto the face of the patient and the level is moved until the laser’s vertical line is on the patient’s median plane and the horizontal line crosses the external auditory canals. Next, a skin marker (i.e., a pen) is used to delineate six points on the skin of the face, establishing the orientation of the reference lines directly onto the patient. Following this, radiopaque markers are tapped on the skin markings and the patient is CT scanned. After scanning, the markings are used to build an anatomical frame of reference. Unfortunately, this method has not been formally validated. A theoretical disadvantage is that it relies on skin landmarks that can be easily displaced.
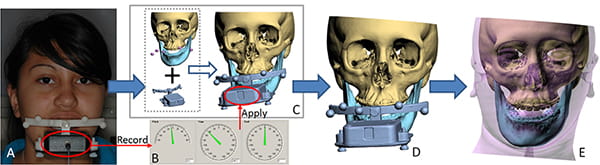
The third method of reorienting a CT to the NHP uses an orientation sensor to record the NHP before CT scanning (Figure 23). The sensor is attached to the same bite-jig used for registration. Next, the patient, with the bite-jig between his teeth and the sensor in front of it, stands erect with his head in the NHP. In this posture, the pitch, roll, and yaw of the sensor are recorded. Because the sensor is orthogonal to the bite-jig frame, the orientations of the sensor and the frame are always equal. By establishing the orientation of the sensor while the patient is in the NHP, the orientation of the frame of the bite-jig for the same posture is also established. In the next step, the sensor is detached from the bite-jig and a fiducial facebow is attached orthogonally to the bite-jig, giving the bite-jig frame and the facebow the same orientation.
Subsequently, the patient is CT scanned while holding the bite-jig and facebow. Thereafter, the CT, including the imaged facebow, is segmented and rendered as a 3D model. Finally, the 3D model is rotated until its facebow attains the measured NHP orientation, placing the whole 3D model in the NHP. The advantage of this method is that it has been validated in vitro and clinically.
In conclusion, both methods currently used to erect frames of reference for the head—the anatomic landmark method and the NHP method—have significant limitations. With this in mind, the authors’ laboratory is now developing new methods to calculate the primal frame of reference for the face, with the goal of eliminating errors that result from existing methods.
Planning
In CASS, surgery is planned using a VTO approach, meaning that surgery is simulated until the desired final outcome is attained. Surgical simulation is done on three-dimensional composite models, using specialized software. These programs can perform three basic functions: cutting and moving bones, articulating teeth, and morphing soft-tissue.48
Cutting and Moving Bones
Bone cutting is a computer operation that simulates an osteotomy. The cutting tool can be set as a simple plane or a three-dimensional array of adjacent planes. Both options are customizable for position, orientation, size, and thickness. To make a cut, an operator first sets the cutting tool into the planned osteotomy and then activates the cutting command. This operation separates an object into two new objects that can be distinguished through recoloring or renaming.
Moving bones involves two different types of transformations: translation and rotation. Translation is movement without rotation (i.e., sliding); rotation is turning around a point. During planning, both types of transformations are required. Translation can be made in the direction of the axes of the coordinate systems; whereas, rotation can be made around any pivot point. With the software, the user can select the center of rotation.
Before translating or rotating objects in the computer, sometimes it is convenient to form groups of objects. In computer terms, this is known as object linkage.49, 50 Linkage allows a transformation to be applied to the entire group, as opposed to a single object. One example occurs in single jaw maxillary surgery. In these circumstances, the maxilla is first moved toward the mandible, placing it into final occlusion—usually maximum intercuspation. Next, the maxilla is linked to the mandible, so both can be rotated around the mandibular hinge axis without disrupting the final occlusion. Then the maxilla and mandible are rotated as a group until the maxillary central incisors are placed in an ideal vertical position.
Another example occurs in bimaxillary surgery, wherein the distal mandible is first moved toward the maxilla, placing it into final occlusion; subsequently the mandible is linked to the maxilla, so the maxilla can be moved without disrupting the occlusion. Maintaining the final occlusal relationship throughout all maxillary movements simplifies planning, as the distal mandible will automatically be in final position once the maxillary movements are complete.
Dental Articulation
In traditional planning, final occlusion is established by hand-articulating stone dental models. This maneuver is quick and reliable; early contacts are easily noted, facilitating occlusal adjustments. Yet establishing final occlusion digitally is challenging. Upper and lower digital dental models are images that can overlap. Moreover, in CASS there is no tactile sensation, nor are there real-time collision constraints. For these reasons, placing two dental models into occlusion becomes time consuming. Furthermore, there are uncertainties regarding the best alignment outcome. This is even more difficult when occlusal adjustments and/or dental arch segmentation are required. Although the authors43, 51-54 and others55-57 are working to resolve these issues, our clinical routine presently employs physical models as an intermediate step.
In the current CASS routine, final occlusion is first established on stone models. The models are then scanned in final occlusion, creating a digital-final-occlusion-template (Figure 24). This template is a computer object depicting upper and lower teeth in final occlusion. It has two parts, top (upper teeth) and bottom (lower teeth). Once the template has been created, it is imported into the CASS software, where it is used to align the jaws of the composite model into final occlusion. The alignment is a simple two-step process. First, the template is aligned to one of the jaws. Then, the other jaw is aligned to the template. As in the template, the upper and lower teeth are in final occlusion; aligning one part of the template to one jaw and then the opposite jaw to the template automatically places the jaws into final occlusion.
When the maxilla is the only jaw involved in the surgery, the template is first aligned to the lower teeth and then the upper jaw is aligned to the template. When the mandible is the only jaw involved in the surgery—or when both are—the opposite sequence is undertaken.
When the dental arches need segmentation, the use of a digital template to align teeth into final occlusion is more complicated. This scenario is best illustrated using the following example: a patient who requires a 3-piece LeFort I osteotomy and a mandibular ramus-osteotomy. As before, the occlusion is first established on stone dental models. For this patient, the upper stone dental model is cut into three pieces, and each piece (i.e., segment) is independently moved and articulated into final occlusion. The intact lower arch is used as a guide. The independent movement of each segment changes the size and shape of the upper arch, creating a new intra-arch relationship among the upper jaw segments.
In the next step, one scans the stone dental models, creating a digital-final-occlusion template that not only captures final occlusion, but also depicts the new intra-arch relationship among the upper jaw segments. After importing a digital occlusal-template into the CASS software, the template must be aligned to the upper teeth of the composite model (Figure 25). However, in the case of arch segmentation, the geometries are dissimilar; that is, the template shows the new upper arch alignment, whereas the composite model shows the original condition. In this circumstance, the template is aligned to the upper jaw in two steps. First, the upper teeth of the template are best aligned to the teeth of the upper jaw. Then, the upper jaw of the composite model is sectioned and each LeFort segment is aligned to the template—at its corresponding place. A similar approach is used when the lower arch is segmented.
Soft-Tissue Morphing
Current software packages are capable of simulating soft-tissue changes that occur with the movement of osseous or dento-osseous segments, and they employ different strategies to achieve that goal. The simulation methods must be accurate and fast. Yet attaining both is difficult because these attributes are inversely related; the more accurate the model, the longer it takes to prepare and run. The facial soft-tissue envelope is a heterogeneous structure composed of different types of tissue: skin, fat, connective tissue, muscle, and mucosa, each one with different mechanical properties. 58 Moreover, the properties are complex, as they are non-linear and anisotropic.58, 59
Several models have been used to simulate soft-tissue deformations. They include: empirical-based models,60-63 mass spring models,64-66 finite element models,61, 65, 67-72 and mass tensor models.73, 74
Empirical-based models calculate soft-tissue deformation by using bone-to-soft-tissue change ratios derived from empirical knowledge63 or statistical calculations.60 This method is fast,60, 63 but inaccurate,61, 73 as it does not consider actual biomechanical tissue properties.60, 69, 73
Mass spring models were initially developed for animation by the gaming industry, where rendering speed is more important than accuracy. In a mass spring model, the facial soft-tissue volume is represented as a 3D array of vertices (masses) attached by springs. Though quick, this method lacks biomechanical relevance and clinical accuracy.60, 69, 73
Finite element models divide the entire soft-tissue volume into a large number of geometrically discrete volumes and assign material properties to them.73 These models can vary from simple to complex. The simplest models assign a single homogeneous material property to the entire soft-tissue envelope. The complex models fashion the envelope as a composite with different material properties. Finite element models are more accurate than mass spring models, as they have true biomechanical relevance. However, preparation and computation time for finite element models are significant (usually 20 hours to 3 days, depending on the complexity of the model). The authors’ laboratory has solved this problem by using an eFace-template method to efficiently generate a patient-specific, anatomically-detailed, facial soft tissue finite element model within minutes.75
Finally, mass tensor models—which can be considered a hybrid of mass spring models and linear finite element models—employ a homogenous tissue property. They are reported to have fast computation times and acceptable accuracy.73
Planning Algorithms
Orthognathic surgery is performed to treat deformities that can affect one or both jaws. Planning a single-jaw surgery is simpler than planning a double-jaw operation. The following sections present planning algorithms for single- and double-jaw surgery, beginning with the simplest scenario and ending with the most complex.
Single-jaw Maxillary Surgery
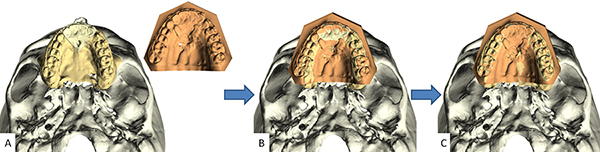
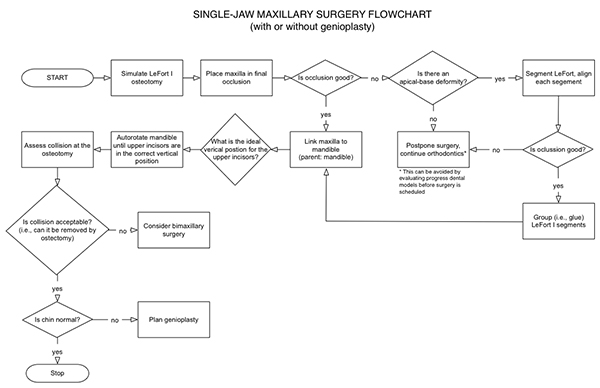
In CASS, the simplest surgery to plan is single-jaw maxillary surgery, an operation that is performed when the maxilla is deformed and the mandible is normal (Figure 26). In this scenario, the planner will make three decisions: final occlusion, vertical maxillary position (i.e., the position of the upper dental midpoint), and an assessment to determine the need for complementary genioplasty.
The surgeon begins the planning process by simulating a LeFort I osteotomy. When the dental arch needs segmentation, the maxilla is cut into two or more pieces. Next, the maxilla is placed into final occlusion by articulating the entire jaw, or its segments, on the mandible. Currently, this is accomplished with the help of a digital-occlusal-template. When the maxilla is cut into pieces, the pieces are rejoined after they have been moved. This allows the maxilla to be moved in the future as a single piece.
Once final occlusion has been determined, the planner links the maxilla to the mandible. Linkage facilitates the next step, autorotation. In autorotation, the mandible is rotated around the condylar axis. Linking the maxilla to the mandible maintains final occlusion during the rotation.
Having already determined the ideal vertical position for the upper incisal midpoint (see the evaluation section), the planner autorotates the mandible until the upper incisal midpoint reaches the desired vertical position. Next, the osteotomy site is assessed. Depending on the maxillary movement, the site may have gaps, butt joints, and regions of overlap.
During surgery, regions of overlap correspond to regions of bony collision. Thus, one should pay particular attention to these areas during the planning process. Note that ostectomies of regions of overlap can prevent collision. Notwithstanding, large areas of overlap in or around the descending palatine artery, pterygoid plates, and the tuberosities are best avoided, as resecting large volumes of bone in these areas is difficult. If the overlap is unacceptable, the planner should consider bimaxillary surgery.
In the final step of planning, a single-jaw maxillary surgery, the surgeon reassesses the chin. Reevaluation is required because chin projection changes with autorotation. If the chin is normal, the plan is finished. If it is abnormal, the planner should simulate and plan a genioplasty.
Single-jaw Mandibular Surgery
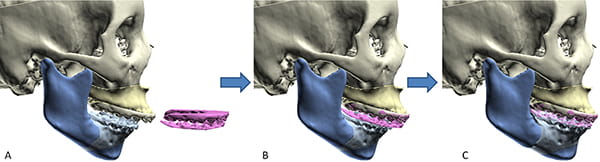
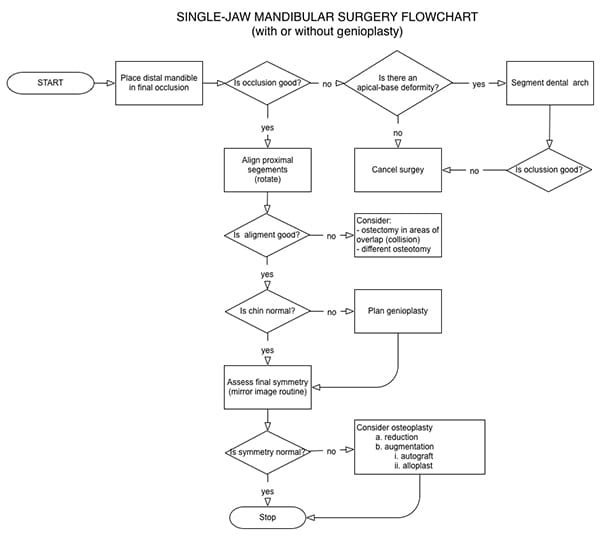
The next most complex plan is single-jaw mandibular surgery, an operation performed when the mandible is deformed and the maxilla is normal (Figure 27). Assuming it involves osteotomies of the mandibular rami (sagittal, vertical, or inverted L osteotomies), one must make four decisions: final occlusion, right proximal segment alignment, left proximal segment alignment, and final symmetry.
In the first step of planning, one simulates the osteotomies, usually in both rami. Sometimes, however, a body osteotomy is also necessary (e.g., segmental dentoalveolar osteotomy, total dentoalveolar osteotomy, or a symphyseal osteotomy. Bilateral ramus osteotomies divide the mandible into three pieces: a distal segment containing the dentition and two proximal segments (right and left), including the condyles.
In the next step, the planner places the dentate segment(s) into final occlusion. Then, the proximal segments are aligned. Each proximal segment is rotated around the center of its condyle until the segment is well aligned with the distal mandible. Ideally, there should be no overlap between the segments, as overlap corresponds to areas of bony collision that can produce proximal segment misalignment at surgery. When overlap is noted, the surgeon should consider ostectomy of the area of overlap or a different osteotomy. Small regions of overlap are amenable to ostectomy; large regions require an alternative operation.
In the following step, the planner reexamines the chin. This is necessary because movement of the mandibular distal segment alters chin position. If the chin is normal, the planner proceeds to the final step; if abnormal, the planner should simulate a genioplasty, moving the chin segment until he/she is satisfied with the outcome.
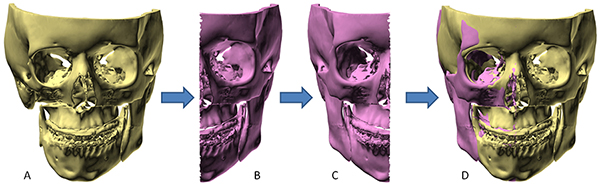
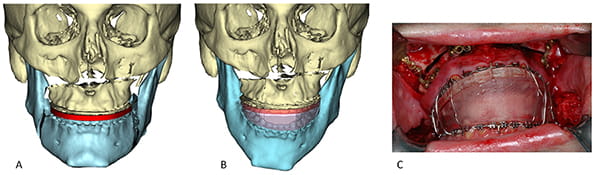
In the last step, the planner assesses final symmetry. When the maxilla is normal and the mandible is abnormal but symmetric, placing the distal mandible in final occlusion maintains symmetry. However, when patients have intrinsic mandibular asymmetry, placing the distal mandible into final occlusion does not correct the asymmetry. Since mild to moderate degrees of intrinsic asymmetry may be imperceptible to the eye, it is important to complete a final symmetry assessment on all patients. This is performed using a mirror-image routine (Figure 28), in which the composite model is cut in half across the median plane. One side is then copied and reflected (flipped) across the median plane, superimposing it over the contralateral half. Subsequently, right-left differences are calculated using a Boolean subtraction—a mathematical method that reveals differences between objects. If the symmetry is good, the plan is complete; if there is residual asymmetry, the surgeon should consider an osteoplasty (reduction or augmentation). The latter can be achieved with bone grafts or alloplasts.
Double-jaw Surgery
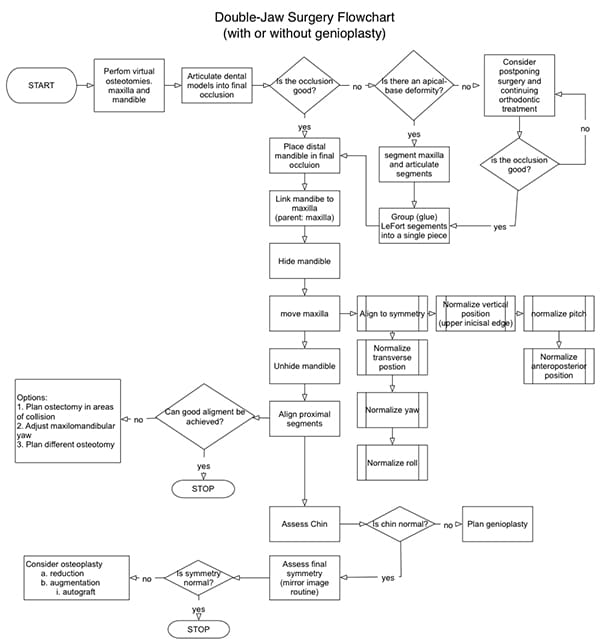
A double-jaw surgery is necessary when both jaws are deformed or when the discrepancy between the jaws is so large that both jaws must be moved, even if one of them is normal. Planning a double-jaw operation is a complex, multi-step process. Planning without having a strategy costs time, produces errors, and results in unsatisfactory outcomes. The authors have developed a planning algorithm to guide surgeons through this process (Figure 29).25, 48
Planning begins by simulating osteotomies in the maxilla and mandible. In the maxilla, one performs a LeFort osteotomy. In the mandible, one usually conducts bilateral ramus-osteotomies, but occasionally, body osteotomies are required as well. If dental arch segmentation is unnecessary, one proceeds to the next step: articulating the maxilla atop the mandible into final occlusion. If arch segmentation is needed, the planner first cuts the jaws into pieces and then articulates each piece into final occlusion. Aligning the jaws into final occlusion is achieved with the aid of a digital-final-occlusion-template.
When the jaws are segmented, one must regroup the segments after they have been moved. Regrouping is the digital equivalent of gluing segments during physical model surgery. It allows reestablishment of the maxilla or distal mandible as a single piece, which facilitates future movements.
The next step is linking the distal mandible to the maxilla. This ensures that the distal mandible moves simultaneously with the maxilla. If the distal mandible is unlinked, the maxilla will move without the mandible, resulting in altered occlusion. Because the jaws are already in final occlusion, it is important to for them to move together.
The mandible is then hidden and the maxilla is moved into ideal alignment. A series of transformations (translations and rotations) is required to reach this alignment; transformations are best done on or around a single point, following a specific sequence. Empirically, the authors have determined that, in order to avoid iterations, the optimal point at which all transformations should be performed is the incisal midpoint. To this end, the authors have established the following planning sequence:
- Symmetric alignment
- Normalization of transverse position
- Normalization of yaw
- Normalization of roll
- Normalization of vertical position
- Normalization of pitch
- Normalization of anteroposterior position
In the first step, the maxilla is symmetrically aligned to the median plane. This involves three transformations: transverse translation, yaw rotation, and roll rotation. Transverse translation places the maxillary incisal midpoint on the median plane. Yaw rotation pivots the maxilla around the incisal midpoint, making the posterior teeth as equidistant as possible to the median and coronal planes. Finally, roll rotation pivots the maxilla around the incisal midpoint until right and left teeth are vertically aligned.
In the second step, the vertical position of the maxilla is normalized. The planner translates the maxilla up or down, placing its incisal midpoint in an ideal position—in relation to the upper lip stomion.
In the third step, one normalizes the maxillary pitch. The planner pivots the maxilla around the incisal midpoint until its pitch is optimized. Maxillary pitch rotation affects the following:
- Inclination of the maxillary central incisors
- Inclination of the maxillary occlusal plane
- Airway size
- Projection of the anterior nasal spine (ANS)
- Chin projection
When deciding the ideal maxillary pitch for a given patient, one should take into account all five of these factors. The first three relate to function, the last two to aesthetics. Frequently, the planner must make compromises among these variables, in accordance with individual case parameters and priorities.
The inclinations of the maxillary central incisors and the occlusal plane are important for disocclusion—the separation of upper and lower teeth during eccentric movement of the mandible. The average inclination of the maxillary central incisors to the horizontal plane is 117.0˚± 6.9˚ for a male and 110.5˚± 9.1˚ for a female.76 The average occlusal plane inclination to the horizontal plane is 9.3˚± 3.8.77 These values are useful when determining the maxillary pitch.
Regarding the airway, decreasing maxillary pitch increases mandibular projection. When the mandible moves forward the tongue moves with it, thereby enlarging the retroglossal airway space; the opposite occurs when maxillary pitch is increased.
Concerning projection of the anterior nasal spine (ANS) and chin, increasing maxillary pitch (by rotating the maxilla around the incisal midpoint) increases projection of the ANS, thereby decreasing projection of the chin. Increasing the ANS projection rotates the nasal tip upward, widening the nasolabial angle; decreasing maxillary pitch has the opposite effect.
The final adjustment required to align the maxilla is focused on the anteroposterior position. The authors leave this adjustment for last because previous transformations can alter one’s decision regarding how much to advance the maxilla. For example, decreasing maxillary pitch or changing its yaw can produce collision between the maxillary tuberosities and the pterygoid plates—collisions that can be easily avoided by advancing the upper jaw.
After the maxilla is in ideal alignment, the mandible is rendered. The distal segment of the mandible will automatically be in final alignment because of its previous linkage with the maxilla in final occlusion. Note that each of the transformations previously applied to the maxilla have been transferred to the distal mandible.
In the following step, the proximal segments of the mandible are aligned. Each proximal segment is rotated around the center of its condyle until the segment is well aligned with the distal mandible. Ideally, there should be no overlap between the proximal and distal segments, as overlap corresponds to areas of bony collision. When present, segment overlap can be mitigated by:
- Readjusting the yaw of the maxilla and distal mandible
- Planning a resection (ostectomy) of the areas of overlap
- Planning a different ramus osteotomy
Readjusting the yaw of the maxilla and distal mandible by one or two degrees can obviate proximal segment collision without altering aesthetics. Adjustments larger than two degrees should be avoided as they can produce buccal corridor asymmetry—the right-to-left difference in the amount of posterior teeth displayed when smiling. To prevent displacement of previous corrections, all yaw readjustments must be made around the upper incisal midpoint.
Small areas of bony overlap are amenable to ostectomy, but large areas of collision that remain after maxillary yaw adjustment can only be avoided by selecting a different operation (e.g., an inverted L osteotomy over a sagittal split).
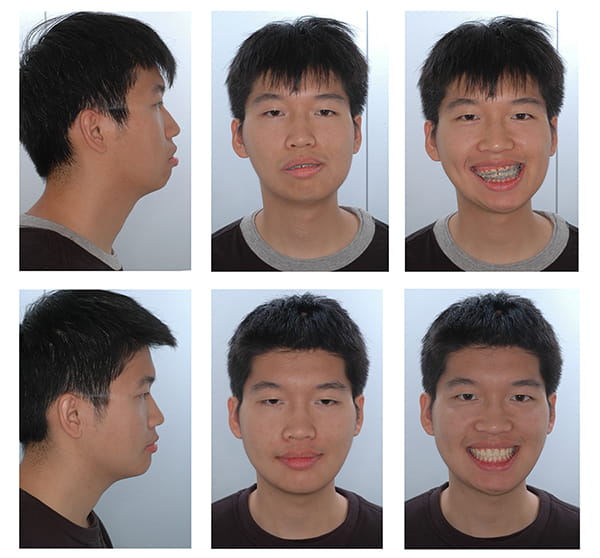
The final two steps: chin assessment and the assessment of final symmetry are the same as those performed for single-jaw mandibular surgery. Figure 30 shows a clinical example of a patient whose bimaxillary orthognathic surgery was planned with CASS.
Preparing for Plan Execution
Planning has no value if the plan cannot be realized at surgery. The ultimate goal is a surgical outcome that is identical to the planned result. In orthognathic surgery, this is attained when the surgeon accurately moves the bone segments to their planned location. Various procedures and appliances have been developed for this purpose and require preparation prior to surgery. In this section we discuss how to prepare for the execution of a surgical plan.
Jaw osteotomies can give rise to two types of movable bone segments: dentate and non-dentate (i.e., with and without teeth). The type and number of segments produced depends on the location of the osteotomies. For example, in a genioplasty, one movable non-dentate segment is created. In a standard LeFort I osteotomy, a single dentate segment is produced. In mandibular rami osteotomies, three segments are created: one distal and two proximal; the distal is dentate; the proximals are not.
During orthognathic surgery, a surgeon must relocate all movable jaw segments (dentate and non-dentate). The new location of the dentate segments is established using occlusal surgical splints. These splints are arch-shaped, removable, plastic appliances placed between the occlusal surfaces of the upper and lower teeth to relocate and temporarily stabilize jaw segments.
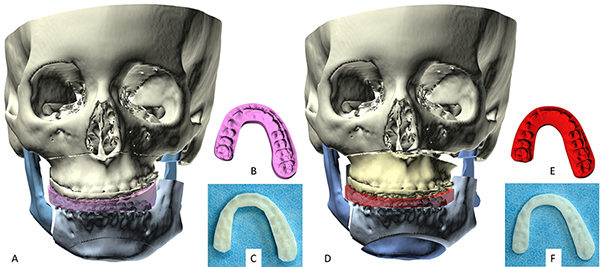
There are two types of occlusal splints: intermediate and final. Intermediate splints are used exclusively in double-jaw surgery, which is performed in sequence (one jaw, then the other). During surgery, the surgeon first cuts and moves one jaw, places it in its new alignment, and fixates it; the same is then done on the other jaw. Intermediate occlusal splints are devices that relate the dentate segments of one jaw—the first to undergo surgery—to the unmoved dentate segment of the other.
Final splints place dentate segments into final occlusion, which is the planned occlusion at the end of surgery. Final splints are needed when the final occlusion is unstable (e.g., prone to slipping) or when interdental osteotomies are used to segment the dental arch (e.g., 3-piece LeFort I, Hofer osteotomy, etc.). They are used in both single- and double-jaw surgery.
In CASS, both types of splints—intermediate and final—are designed in the computer and subsequently fabricated using rapid prototyping techniques.10, 33, 34, 78, 79 To create an intermediate splint, the computer model shows the first jaw in its final alignment and the second jaw in its original condition. If present, collision (i.e., overlap) between the upper and lower teeth is avoided by rotating the mandible open. Next, a three-dimensional arch-shaped pattern is placed between the upper and lower teeth, and the teeth are subtracted from the pattern. The resultant digital splint is then fabricated via rapid prototyping (Figure 31); a non-toxic sterilizable material is used for this purpose. The final splint is created in a similar fashion, with the exception that the computer model is placed in final occlusion, for the final outcome (Figure 31).
When double-jaw surgery involves segmentation of the dento-alveolus of the first jaw, the use of separate—intermediate and final—splints is time consuming. In such cases, a surgeon performs the following steps:
- Cuts the first jaw, creating two or more dento-osseous segments
- Locates and wires each of the dento-osseous segments into the intermediate splint
- Places the splint on the opposite jaw (uncut jaw)
- Wires upper and lower teeth together, using maxillomandibular wires
- Fixates the first jaw, using plates and screws
- Removes the wires and the intermediate splint
- Cuts the second jaw
- Wires each of the dento-osseous segments of the first jaw into the final splint
- Places the dentate segment of the second jaw into the final splint
- Wires upper and lower teeth together, using maxillomandibular wires
- Fixates the second jaw
In these cases, using a sandwich occlusal splint rather than separate intermediate and final splints, simplifies and shortens surgery. A sandwich occlusal splint is a two-part splint made by interlocking final and intermediate splints. This splint is fabricated in the following fashion. First, a regular final splint is fabricated with both jaws in their final position (Figure 32A). Next, the second jaw on which surgery will be performed is rendered in its original form (uncut) while the final splint is left on the segmented first jaw. Then, the bite is opened to avoid collisions and the intermediate splint is fashioned between the final splint and the uncut jaw (Figure 32B).
When using a sandwich splint, the surgeon:
- Cuts the first jaw, creating two or more dento-osseous segments
- Locates and wires each of the dento-osseous segments into the final splint
- Places the intermediate splint between the final splint and the opposite jaw
- Wires upper and lower teeth together, using maxillomandibular wires
- Fixates the first jaw, using plates and screws
- Removes the wires and intermediate splint
- Cuts the second jaw
- Places the dentate segment of the second jaw into the final splint
- Wires upper and lower teeth together, using maxillomandibular wires
- Fixates the second jaw
A sandwich splint eliminates one step: wiring each of the dentoalveolar segments (of the first jaw) into the intermediate splint—a task that is tedious and time consuming. Figure 32C shows the intraoperative use of a sandwich splint. The photo shows the final splint stabilizing three maxillary dentoalveolar segments and the intermediate splint—located between the final splint and the lower jaw—thereby relocating the upper jaw.
Occlusal splints place dentate-osteotomy segments into planned alignment. These devices are all one needs to reposition the dentate segments of the mandible, but they are insufficient for the maxilla. In maxillary surgery, the upper jaw is articulated against the mandible, a movable bone. A cut upper jaw moves even when wired to the mandible. Thus, for maxillary surgery, one requires additional methods to set the maxilla into final alignment. In addition to using splints, surgeons restrict mandibular movements to rotation by placing the mandible in centric relationship; vertical maxillary position is controlled by using intraoperative measurements.
At surgery, before cutting the upper jaw, a surgeon inserts a K-wire into the nasal bones. From this external reference, the baseline vertical maxillary position is established by measuring the distance between the K-wire and the upper incisal midpoint. Next, the target vertical position is calculated by adding or subtracting the planned vertical change to or from the baseline measurement. After mobilizing the maxilla and wiring it to the mandible, the mandible is placed into centric relationship and the maxillomandibular complex is rotated up or down until the upper incisal midpoint reaches the target distance. In this position, the maxilla is fixated.
In orthognathic surgery, non-dentate segments arise in the mandible after osteotomies of the rami or chin. The non-dentate proximal segments of mandibular ramus osteotomies (sagittal split, vertical, or inverted L) reach their final alignment when the relationship between the proximal and distal segments visualized in CASS is reproduced at surgery.
During the operation, the surgeon reviews images of the planned outcome showing the relationship between the proximal and distal segments. Simultaneously, he manipulates a given proximal segment until the planned relationship is attained. This may involve resecting bone in areas of overlap and/or creating gaps between the segments. CASS facilitates these maneuvers by mapping and quantifying these areas in advance.
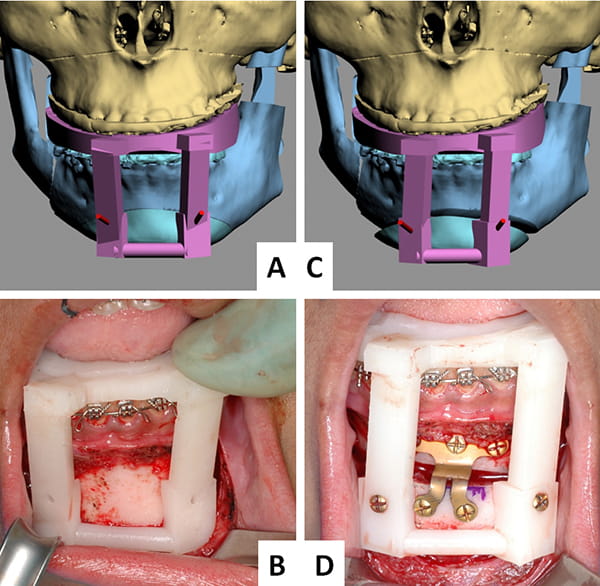
With genioplasty, surgeons can relocate the chin segment, either in freehand or with templates. The freehand method is the same as that described above for the mandibular proximal segment: the surgeon attempts to reproduce on the patient what is seen in CASS. The template method uses surgical templates to place the chin in its new alignment. Surgical templates are removable appliances that relocate and stabilize a non-dentate bony segment; they relate the planned position of the movable segment to adjacent segments.
Investigators at Houston Methodist Hospital in Texas developed the first known chin-template system (Figure 33).10, 34 This system uses two templates: a marking template and a positioning template. Both relate the chin to the lower teeth. The marking template (Figure 33A and B) is employed first. It marks the position and orientation of two pilot-holes that are drilled on each side of the chin. After completion of the osteotomy, a surgeon places the positioning template (Figure 33C and D) on the lower teeth and aligns the chin to the template. The chin is then temporarily fixated to the template using two 2mm (diameter) screws, which are inserted through the template into the previously drilled pilot-holes. Next, the surgeon installs a chin plate for permanent stabilization; finally, the positioning template is removed.
Table of Contents